Many-body Physics with Trapped Ions
When ions are laser cooled to temperatures in the mK range, they freeze out in crystalline structures, so-called Coulomb crystals. In these crystals the ionized atoms can be resolved individually by means of their fluorescence, see Fig.1. Depending on the trapping parameters the crystals take on different phases in one to three dimensional structures. When a symmetry breaking phase transition is crossed non-adiabatically, i.e. faster than the speed of sound in the crystal, topological defects can occur [1]. Then the ions cannot communicate the new configuration they take on and different domains are formed inside the crystal with incompatible orientation. The resulting defects have the physical properties of discrete solitons and show a highly nonlinear behavior [2-4].

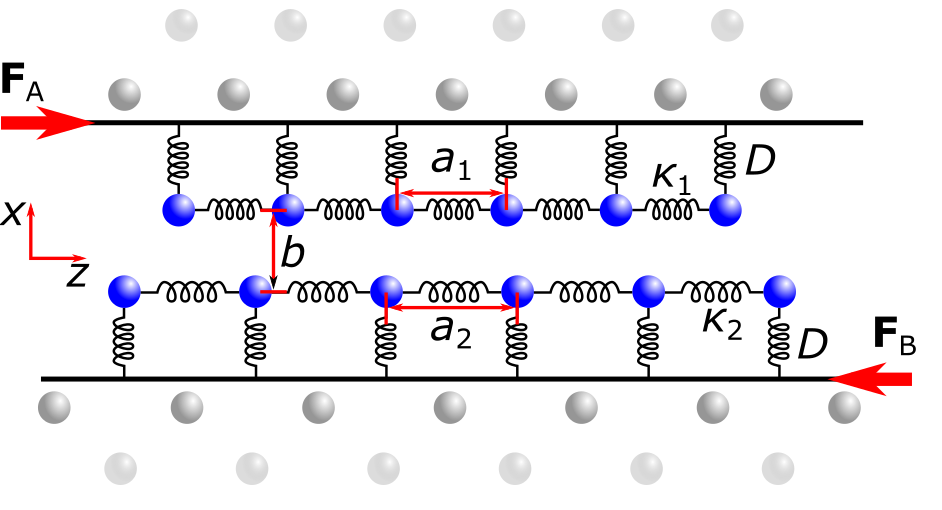
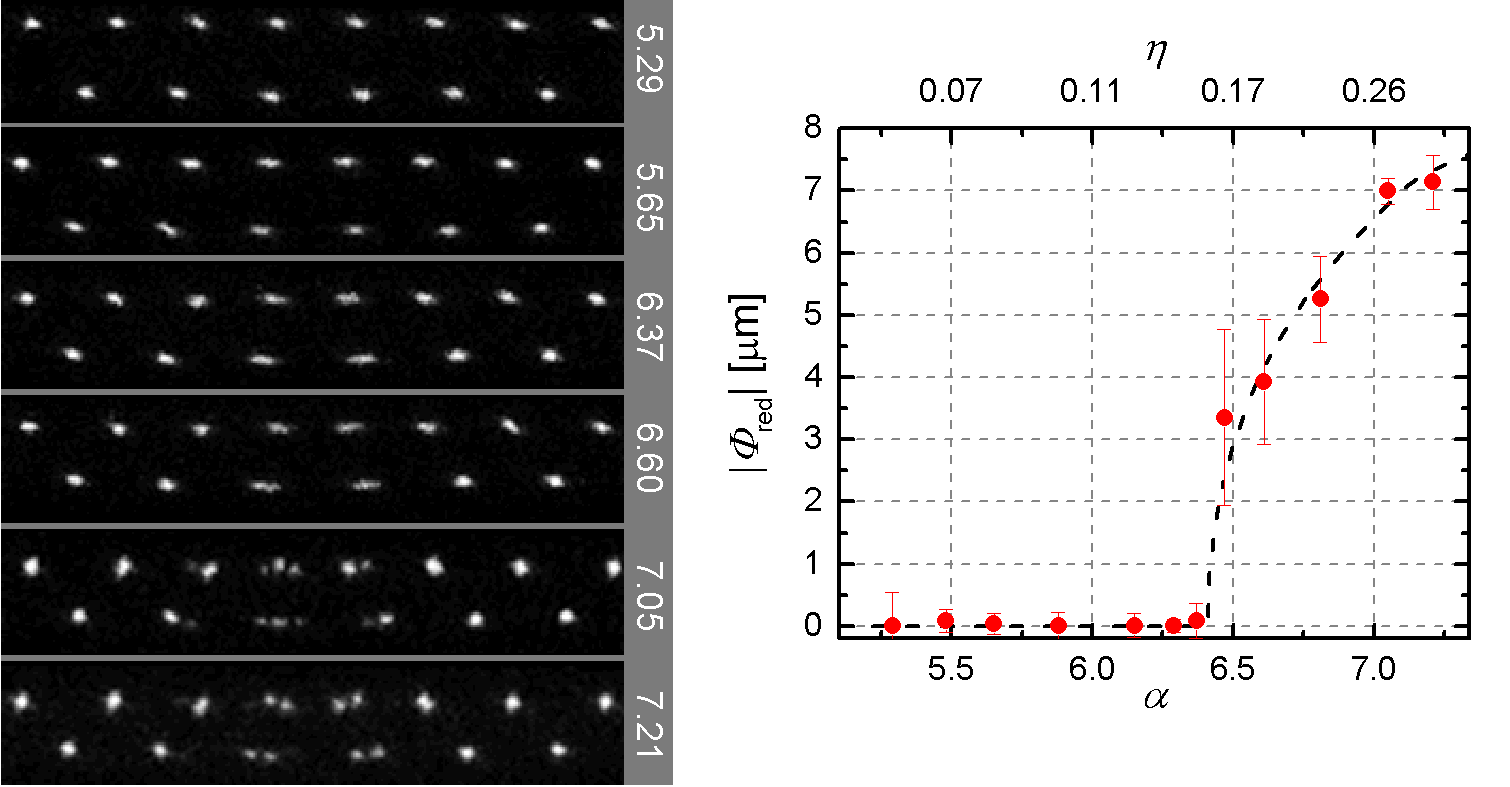
Preparing a two-dimensional Coulomb crystal as shown in Fig. 1(e), nanofriction in a self-organized system can be studied on atomic scale. This system can be viewed as two linear chains sliding against each other. This model system contains identical particles that are joined by interatomic springs, see Fig. 2. If the crystal features a topological defect, its local disturbance causes different intra-ion distances for the two ion chains. Varying the radial spacing between the atomic layers, a symmetry breaking phase transition, the so-called Aubry-type transition, can be observed (see Figure 3) [5]. At this transition the motion changes from sticking to sliding, which changes the frictional properties of the ion chains.
As the formation of topological defects occuring in phase transitions is a universal phenomenon [6], the behavior of our crystals can be transferred to various other systems in nature, from solid-state to cosmological systems. In particular, the interaction of two ion chains with back action is similar to the dynamics of biomolecules, like the DNA strands.
The most important results can be found here.
See also:
Atomare Reibungseffekte
Cosmology in the lab using laser-cooled ions
References
[1] Pyka et al., Nat. Commun.4, 2291 (2013)
[2] Partner et al., New J. Phys.15, 103013 (2013)
[3] Landa et al., Phys. Rev. Lett. 104, 043004 (2010)
[4] Partner et al., Physica B 460, 114-118 (2015)
[5] Kiethe et al., Nat. Commun.8, 15364 (2017)
[6] del Campo et al., J. Phys.: Condens. Matter25, 404210 (2013)
[7] Timm et al., Phys. Rev. Research 2, 033198 (2020)
[8] Kiethe et al., Phys. Rev. B 103, 104106 (2021)
[9] Timm et al., Phys. Rev. Research 3, 043141 (2021)
